La presente es una republicación del artículo homónimo incluido en la edición 320, págs. 8 a 13, a fin de corregir errores de dicha oportunidad
Aspectos teóricos y sus aplicaciones prácticas
En esta nota técnica, tratamos los siguientes tres temas:
-
Medición de la resistencia de la puesta a tierra (RX) de un electrodo dispersor X por el método de la caída potencial
-
Mediciones de la resistencia de puesta a tierra RX con un telurímetro de cuatro bornes C1 P1 P2 C2 para las disposiciones XPC y XCP
-
Guía de mediciones de resistencias de puesta a tierra (Rpat) por el método de la caída de potencial (caída de tensión)
Se trata de distinguir las mediciones de las resistencias de puesta a tierra (RX) de electrodos X en los casos que sean: a) iguales o mayores que un ohm (1 Ω); b) menores a un ohm (1 Ω) tal como lo indican las normas técnicas citadas.
Medición de la resistencia de la puesta a tierra (RX) de un electrodo dispersor X por el método de la caída de potencial
Electrodo X puntual
El electrodo X se dice “puntual” cuando sus dimensiones enterradas en el suelo (o en la roca) son muy pequeñas comparadas con las distancias a que se colocan los electrodos auxiliares P de potencial y C de corriente, necesarios para medir RX con un telurímetro (o con instrumental voltamperimétrico). 
Tabla 1. Potenciales absolutos V de los electrodos X y P
Principio del método
El generador produce una tensión Eg cuya forma de onda temporal Eg(t) y su valor eficaz Eg son tales que la corriente generada I entra al electrodo a medir X (corriente +I), pasa por el suelo y retorna por el electrodo C al generador G (corriente -I que sale del suelo y vuelve al generador G).
El electrodo de corriente (C) se coloca a una distancia (D) del electrodo X cuya RX deseamos medir. Así se tiene: D = |XC|
Se coloca el electrodo P de potencial a una distancia X del electrodo X tal que: X = |XP|.
El amperímetro (A) mide el valor eficaz de la corriente (I) y el voltímetro (V), el valor eficaz de la ddp U entre los potenciales de P y de X (que producen corrientes +I y -I en el suelo).
Las corrientes +I y -I generan los cuatro potenciales absolutos V con respecto al SEN (suelo eléctricamente neutro, IRAM 2281-1, 3 y 4) o tierra de referencia (IRAM 2282-4).
En la tabla 1 se indican los cuatro potenciales que producen la corriente +I entrante al X y la -I saliente del C.
El electrodo X se considera “puntual”, como así también los electrodos auxiliares C y P.

Figura 1. Esquema electrogeométrico del principio del método de la caída de potencial para la medición de la resistencia RX de puesta a tierra del electrodo puntual X, con la disposición XPC de los electrodos puntuales X, P y C
El potencial total del electrodo X es:
VX = (X; X) + V (X; C) [1]
Aplicando la teoría del electrodo dispersor hemisférico enterrado en un suelo (o roca) homogéneo de resistividad volumétrica ρ (Ωm) constante tendremos que es:
V (X; X) = RX I [2]
siendo RX la resistencia de dispersión o de puesta a tierra del electrodo X que vamos a medir. Además, el electrodo C con su corriente (-I) produce en X, el potencial
V (X; C) = (ρ X(-I)/2π) (1/D) = (ρI/2π) (- I/D) [3]
En [1] reemplazamos las expresiones [2] y [3], resultando:
VX = RXI + (ρI/2π) (-1/D) [4]
El potencial total VP del electrodo auxiliar P es:
VP = V (P; C) + V (P; X) [5]
Los potenciales componentes de VP son los siguientes:
V (P; C) = (ρ (-I)/2π) (1/D-X) = (ρI/2π) (-I/D-X) [6]
V (P; X) = (ρ(+I)/2π) (1/X) = (ρI/2π) (1/X) [7]
Llevando [6], [7] a la [5], sale:
VP = (ρ (-I)/2π) (1/X – 1/D-X) [8]
La caída de potencial es la diferencia de potencial siguiente:
La ddp U = ddp (X; P) = VX – VP [9]
Llevando los valores de los potenciales totales según [4] y [8] a la [9], resulta:
U = VX – VP = [RXI – (ρI/2π (1/D)] – [(ρI/2π 1/X) - (ρI/2π) (1/D-X)] [10]
De la [10] hallamos la ecuación de la ley de Ohm clásica:
U/I = RX – ρI/2π (1/D + 1/X – 1/D-X) [11]
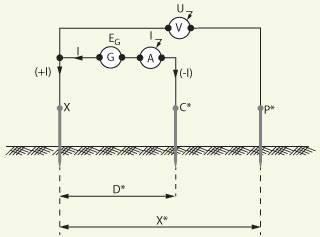 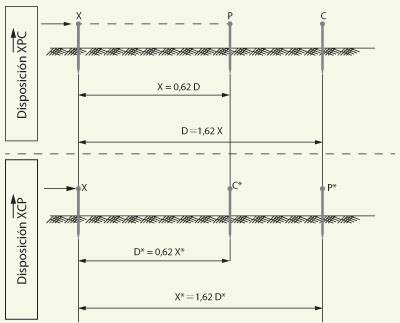
Figura 2. Disposición XCP de los electrodos puntuales X (a medir), C (corriente) y P (pontencial) para medir la resistencia de puesta a tierra RX del electrodo
Figura 3. Mediciones de la resistencia de puesta a tierra del electrodo puntual X mediante los electrodos puntuales P (de potencial) y C (de corriente) con un telurímetro de tres o de cuatro bornes, siendo: D, la distancia entre X y C (para XCP), y X, la distancia entre X y P (para XPC)
Observamos que U/I difiere de RX en la expresión del paréntesis. Si se elige X tal que se anule esa expresión del paréntesis, tendremos ese caso ideal en el que se cumple que:
U/I = RX [12]
que es el valor buscado, pero observemos que siempre será U/I menor o igual que RX en la práctica.
Resolviendo la ecuación del paréntesis de [11], ella se reduce al numerador siguiente:
F (X) = X2 + DX – D2 [13]
Las raíces de [13] son
X/D = (-1 ± √5)/2 = 0,618; -1,618 [14]
La raíz positiva X/D = 0,618 nos indica que P debe colocarse al 62 por ciento de la distancia (D) midiendo desde X hacia C, es decir, en el orden XPC.
Disposición XCP de los electrodos X (a medir), C (de corriente) y P (de potencial)

Tabla 2
En este caso, las ecuaciones son
VX = V (X; X) + VX; C [15]
siendo
V (X; X) = RXI [16]
V (X; C) = ρ (-I)/2π (1/D) = ρI/2π (-1/D) [17]
Vp = V (P; C) + V (P; X) [18]
siendo
V (P; C) = ρ (-I)/2π (1/X-D) = ρI/2π (-1/X-D) [19]
V (P; X) = ρ (+I)/2π (1/X) = ρI/2π (1/X) [20]
VP = ρI/2π (-1/X-D + 1/X) [21]
La ddp U = VX – VP resulta la siguiente:
U = VX – VP = RXI - ρI/2π [(-1/D) - (-1/X-D) + (1/X)] =
=RXI + ρI/2π [(1/D) - (1/X-D) + (1/X)] [22]
Para anular la expresión del paréntesis de [22], procedemos así:
1/D + (-1/X-D) + 1/X = [(X-D) X – DX + D (X-D)] / [D (X – D) X]
X2 – DX – DX + DX - D2 = 0
X2 +DX – D2 = 0
(X/D) 2 – (X/D) – 1 = 0
X/D = (1 ± √5) / 2 = 1,618; -0,618

Figura 4. Disposiciones de los electrodos X, P, C y los conexionados del telurímetro C1 P1 P2 C2 para esas disposiciones.
Mediciones de la resistencia de puesta a tierra RX con un telurímetro de cuatro bornes C; P1; P2; C2 para las disposiciones XPC y XCP
En la figura 3, representamos a los tres electrodos X (a medir), P (potencial) y C (corriente) en los dispositivos XPC (arriba) y XCP (abajo), con sus distancias y sus interpretaciones según la tabla 2.
En la figura 4, representamos a las disposiciones XPC y XCP con los conexionados del telurímetro C1 P1 P2 C2 correspondientes a esas disposiciones para medir RX.
Guía de mediciones de resistencias de puesta a tierra (Rpat) por el método de la caída de potencial (caída de tensión)
Telurímetro de lectura directa de cuatro bornes C1 P1 P2 C2
En la figura 5, representamos un esquema del principio de medición de una resistencia de puesta a tierra RX del electrodo X dibujado por su símbolo gráfico eléctrico general (una raya vertical centrada en tres rayas horizontales de largos decrecientes y equidistantes).
Normas técnicas aplicables a la medición de resistencia de puesta a tierra. Método de la caída de potencial (o de caída de tensión)
En la norma argentina IRAM 2281-2:2002 “Guía de mediciones de magnitudes de puesta a tierra (resistencias, resistividades y gradientes)”, en su apartado 6.2.4 se trata el método de la caída de tensión (o de potencial). El apartado 6.2.4 tiene once párrafos (o puntos) 6.2.4.1-11 y las figuras 3, 4, 5 y 6.
En British Standard BS 7430:1991 “Code of practice for earthing” se trata el método de medición de la resistencia de puesta a tierra en sus apartados 16.2 (con 16.2.1 y 16.2.2, figuras 11 y 12).  
Figura 5. Esquema de principio de medición de RX del electrodo X con un telurímetro de lectura directa con cuatro bornes C1 P1 P2 C2 para la disposición XPC de los electrodos
Figura 6. Ejemplo de distancias XPi en función de la distancia paramétrica XC (fijada) para medir la resistencia de puesta a tierra = RX mayor a un ohm de un electrodo X (jabalina, cable horizontal, etcétera), siendo:
XP1 = XC/2 para medir RX1 (ohm) [a]
XP2 = XC/2 + 7 m para medir RX2 (ohm) [b]
XP3 = XC/2 – 7 m para medir RX3 (ohm) [c]
Nota: ver el esquema de medición de la figura 5.
Medición de la resistencia de puesta a tierra RX de un electrodo (jabalina, cable vertical u horizontal enterrado, etcétera) siendo su resistencia mayor a un ohm, mediante telurímetro
Según BS 7430:1991 (apartado 16.2.2), para medir la RX de un electrodo X que sea mayor a un ohm, se clava el electrodo auxiliar de corriente C a una distancia XC mayor o igual a treinta a cincuenta metros, que queda fija. Se efectúan tres mediciones de RX (ver figura 6) con el electrodo P en tres ubicaciones P1, P2, P3, siendo:
RX1 a la distancia XP1 = XC/2 [a]
RX2 a la distancia XP2 = (XC/2) + 7 m [b]
RX3 a la distancia XP3 = (XC/2) – 7 m [c]
Se calcula el promedio RX = (RX1 + RX2 + RX3) / 3
Si cualquier valor RXi medido cumple con la condición de una aproximación al cinco por ciento de RX, es decir, RXi es menor o igual a RX ± 0,05 RX, se da por aprobada la medición. En caso contrario, se debe aumentar XC y volver a medir RX otra vez (u otras veces).
Mediciones de resistencia de puesta a tierra menor a un ohm
Se tratan en las normas argentina IRAM 2281-2 (apartados 6.2.4.5/11) y británica BS 7430:1991 (apartado 6.2.2 y figura 12).
Mediciones de RX con las disposiciones XPC (figura 4a) y XCP (figura 4b)
Si los valores de RX (XPC) y RX (XCP) están dentro de un cinco por ciento de su promedio RX, siendo RX = ½ • [RX (XPC) + RX (XCP)], es decir, que RX (XPC) = RX ± 0,05 RX y que RX (XCP) = RX ± 0,05 RX, el resultado de ambas mediciones se considera prácticamente válido porque las distancias X = XP y D = XC elegidas para la medición son suficientes para que los tres electrodos X, P y C no interfieran entre sí tanto como para que perturben la medición telurimétrica cuyo principio electrofísico es que X, P y C deben ser prácticamente puntuales, lo que depende de las distancias XP y XC (para XPC) y XP y XC (para XCP).
Bibliografía
[1] Arcioni, Juan Carlos. (2006 y 2009): "Puestas a tierra de instalaciones y sistemas eléctricos de baja tensión, media y alta tensión". Jorge Sarmiento, Córdoba
[2] IRAM. (2002) 2281-2 (2016/2017 en revisión), BSI (1991) BS 7430
Nota del autor:
El autor aprendió el método citado en el último párrafo con el querido colega Prof. Ing. Ilmar Manifesto, exjefe del Laboratorio Electromecánico de Explotación, de SEGBA (1958-92) durante sus trabajos (1961-92) en esa empresa para las mediciones de puesta a tierra. Vaya esta nota técnica como el agradecimiento del autor y en feliz memoria a la persona del distinguido colega y amigo fallecido en esta década. |